By Carrie Bengston and Arwen Cross
Every time you sneeze, droplets of snot shoot out of your nose and mouth (that’s why you should cover your mouth when you sneeze). But did you know droplets are roughly spherical and you need π to describe their shape?
Today is pi day because the date is written 3.14 in some parts of the world. So we’re bringing you an example of how our researchers use π.
When you sneeze, small droplets come out of your nose and mouth. They’re roughly spherical. Photo by Public Health Image Library.
Our mathematicians are interested in droplets. But Benny Kuan and Peter Witt aren’t studying snot, they’re studying droplets of hot magnesium. Their work will help perfect a new way of producing magnesium called MagSonic.
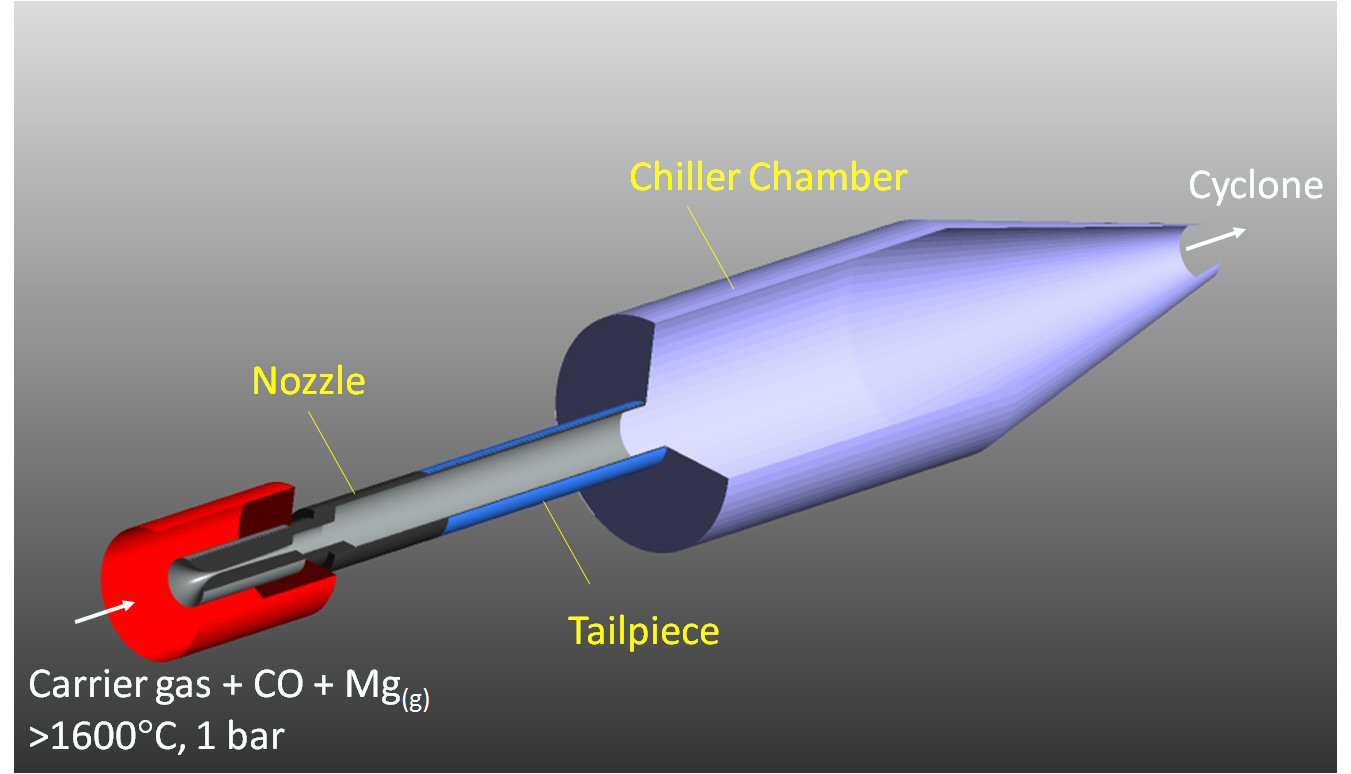
MagSonic works by blasting hot magnesium gas out of a nozzle at four times the speed of sound (over a kilometre per second) and allowing it to cool in a vacuum at a rate of more than a million degrees Celsius per second. The magnesium gas condenses to form liquid droplets before solidifying into powder.
MagSonic purifies magnesium more efficiently than existing methods, so the MagSonic team leader Leon Prentice and his team won the 2013 Vittorio de Nora prize for Environmental Improvements in Metallurgical Industries.
Producing magnesium efficiently is important because we use the metal for many purposes. These include alloys of magnesium and aluminium for lightweight applications like building aircraft and rockets, in certain batteries and as an additive in steel.
Cut away diagram of the MagSonic™ Rig showing the nozzle and chiller chamber.
π is a key character in the MagSonic story, because when you’re making magnesium using MagSonic you have to be careful that the reactor doesn’t get blocked with metal. This depends on how quickly the magnesium gas condenses and solidifies as it comes out of the Laval nozzle. π comes in because the calculations about condensing droplets assume they’re spherical (although in practice they’re often ellipsoidal shaped).
Our mathematicians Benny and Peter are using mathematical modelling to optimise the shape of the Laval nozzle and the MagSonic reactor. How fast the droplets condense, and whether they do that in the nozzle or after they’re sprayed out, depends on lots of things including the shape of the Laval nozzle.
In the MagSonic process hot gas moves at supersonic speed through the nozzle and then condenses and solidifies. The shape of the nozzle determines the rate at which the gas accelerates to and beyond the speed of sound. The speed of the gas is one of the factors that affects how fast it condenses.
π appears frequently when you calculate parameters like the speed of the droplets and the rate of nucleation and condensation. That’s because the spherical droplet’s surface area, volume and cross-sectional area are needed to calculate several things. These include the drag on droplets, how heat is transferred between the droplets and the gas, and whether the droplets grow in size as they condense.
Any high school student can tell you that you calculate the volume of a sphere by cubing its radius and multiplying by π and by four thirds (volume = 4/3 π r3). You can apply similar equations to the magnesium droplets condensing from gas.
Benny and Peter used these equations in their computer models to design nozzles for MagSonic. Then Leon and their other colleagues in the lab tested the new nozzle designs.
Now they’ve got a MagSonic reactor that doesn’t get blocked – thanks to π, computer modelling, and experimentation.
Benny Kuan demonstrating some of the equations he used for the MagSonic project.
Benny says he never thought the strange, irrational number he learnt at school would be so useful in his job doing maths for light metals research – but it is !
Thank you π!
A few facts about π
- π is irrational, so if you try to calculate it precisely, the decimal places never stop or repeat.
- People memorise it for fun – the record is currently 67 890 memorised digits.
- π was known in ancient Egypt and Babylon, but the Greek scholar Archimedes developed the first rigorous approach for calculating π (using polygons).
- The Greek letter π has only been used to represent π since the mid-18th century.
Read more
Check out the pi day activities on the Helix Blog and read more about π fun via the Maths of Planet Earth site.